INTEGRAL KALKULUS
pengertian Integral merupakan bentuk operasi matematika yang menjadi kebalikan (invers) dari operasi turunan dan limit dari
jumlah atau suatu luas daerah tertentu. Berdasarkan pengertian tersebut
ada dua hal yang dilakukan dalam integral sehingga dikategorikan menjadi
2 jenis integral. Pertama, integral sebagai invers/ kebalikan dari
turunan disebut sebagai Integral Tak Tentu. Kedua, integral sebagai
limit dari jumlah atau suatu luas daerah tertentu disebut integral
tentu.
integral kalkulus atau integrasi adalah kebalikan dari
differensiasi, yaitu:
- Apabila fungsi F(x) merupakan an integral (anti derivative) function dari fungsi f(x), maka : F(x) disebut sebagai primitive function, sedangkan
- f(x) merupakan derivative dari F(x) dan f(x) adalah fungsi kontinyu (a continuous function) di atas domainnya atau suatu interval independent variabel x.
- Jadi integrasi atau integral kalkulus menyangkut pencarian (tracing) asal (the parentage of) dari fungsi f(x). Tetapi differensiasi mencari turunan (derivative atau differentiation) dari F(x).
- Differensiasi dari F(x) menghasilkan fungsi yang unik (a unique derivative function) f(x).
- Sebaliknya, integration dari f(x) menghasilkan banyak tak terbatas bentuk fungsi (indefinite number of possible parents) F(x).
Integral adalah kebalikan
dari differensial.
Notasi:
- f(x) adalah fungsi yang akan diintegralkan
- dx tanda untuk melakukan diferensiasi terhadap x
- → notasi diferensiasi dari the primitive function.
rule 1 (The power rule)
“n” sebagai pangkat dari x , dimana n tidak boleh bernilai -1. Karena nantinya pembaginya -1 + 1 = 0, Bilangan berapa pun jika dibagi 0 hasilnya tak terdefinisi/ tak hingga
Contoh soal :
- Rule 2 (The exponential rule)
Fungsi eksponensial adalah fungsi yang biasa dinotasikan
dalam bentuk (e pangkat x).
- Rule 2a
- Rule 2b
Contoh Soal :
Rule 3 (The logaritmic rule)
Logaritma adalah operasi matematika yang merupakan kebalikan
(atau invers) dari eksponen atau pemangkatan.
- Rule 3a
Rule ini bentuk spesial (a special form) dari the power
function xn karena untuk n = 1 tidak bisa dilakukan atas
dasar Rule 1 (the power rule) sebab menjadi 1/0 = ∞
-Rule 3b
Contoh Soal:
Rule 4
Contoh Soal
Rule 5
Contoh Soal :
RULE 6
Teknik perhitungan integral pada rule ini:
1. Memilih fungsi u : g(x) sehingga ∫f (g(x)) g'(x) dx dapat diubah menjadi ∫f (u) du.
2. Tentukan fungsi integral umum = f (u) yang bersifat f’ (du) : f (u).
1. Memilih fungsi u : g(x) sehingga ∫f (g(x)) g'(x) dx dapat diubah menjadi ∫f (u) du.
2. Tentukan fungsi integral umum = f (u) yang bersifat f’ (du) : f (u).
Contoh soal:
RULE 7
contoh soal:
RULE 8
Sifat-sifat :
Contoh soal:
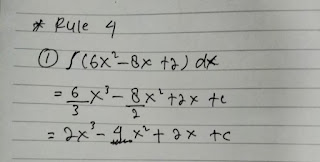
Komentar
Posting Komentar